
 Hello everyone! For this month’s lesson I decided to break things up a little bit and get away from the typical wheedly-deedly lead guitar type of lesson and talk about some rockin’ rhythm guitar ideas!
Hello everyone! For this month’s lesson I decided to break things up a little bit and get away from the typical wheedly-deedly lead guitar type of lesson and talk about some rockin’ rhythm guitar ideas!
We have to do something to pass the time in between our solos, right?
So grab your guitar, check out these ideas and get ready to create some killer rhythm riffs of your own! Feel free to use these ideas as springboards for your own songs.
Is It Magic?
When you listen to songs by popular rock, pop and metal bands have you ever felt like all of the chords seem to fit together well? It’s almost as if they have some divine gift that helps them to choose the right chords!
There’s a good reason for this. Generally speaking, songs or riffs that sound pleasant to our ear use chords and notes that are “diatonic” to a particular key. Don’t get hung up on jargon, this just means that all of the chords work together in a particular key.
So when you hear a song that sounds good the writer may have a good knowledge of music theory which he used to help him to choose the chords in his (or her) song.
Note: I said “generally speaking” above because today our ears are becoming more accustomed to hearing adventurous harmonies and chord progressions than past generations. A few centuries ago some intervals commonly used today would have caused you to be burned at the stake! (Seriously…)
I don’t want to dig deep into theory in this lesson – instead I want to give you some quick and easy to use tools to immediately start crafting your own songs.
Dropped-D Tuning
These examples are all in Dropped-D tuning. For those of you unfamiliar with this tuning, it is similar to normal tuning, except that the low E-string (6th string – the fattest one) is tuned to D (one whole step down). If you have a common chromatic electronic tuner, you can accomplish this pretty easily.
So are you tuned up and ready to go? All right then, let’s continue!
One of the coolest things about Dropped-D tuning is that it allows you to play power chords (aka 5th chords) on the low E and A strings by barring one finger. This allows you easily change chords and slide between them.
Also, if you strum your open (unfretted) 6th and 5th strings together you get a nice thick, powerful-sounding D power chord!
Power Chord Scales
So let’s take a look at what I like to refer to as dropped-D power chord scales – essentially a map of the power chords in the key of D. By using these chords together you can easily create your own great-sounding riffs and songs.
Figure One demonstrates our first chord scale pattern – the D Blues Scale on the 6h string.

Figure 1: D Blues Scale on low E-string
Our next figure is also the D Blues Scale, only this time on the 5th string.
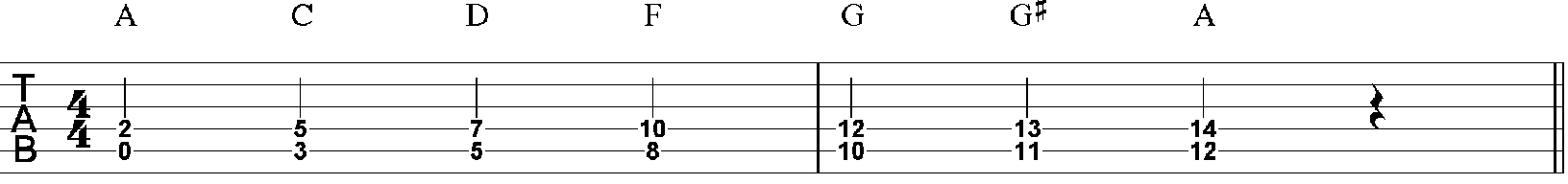
Figure 2: D Blues Scale on A-string
Now let’s apply some simple rhythmic ideas to our first chord scale pattern and see what we can come up with…
In Example One we play each chord followed by two palm muted open (D) power chords in an 8th-note triplet rhythm. It’s surprising how great this simple pattern sounds!
Example One:

![]()
Note: You can get a free Guitar Pro Tab of this lesson, along with audio clips, a drum track to practice with and more free high quality guitar lessons like this one at: http://paultauterouff.com/freeguitarlesson.php
Example Two applies the same basic idea from above to the chords on the 5h string. Again – the results sound awesome!
Example Two:


Another Power Chord Scale
So now let’s take a look at another scale commonly used in rock and metal music. Figure Three demonstrates a power chord scale based on the notes of the D natural minor Scale on the 6th string.

Figure 3: D Natural minor Scale on low E-string
Figure 4 is the same power chord scale as above, just moved over to the 5th string.

Figure 4: D Natural minor Scale on A-string
In the next example I play a different three-note riff – two fretted notes followed by a palm muted open (D) power chord. Note how the open chord occurs at different places from one measure to the next. Cool? Yes!
Example Three:

![]()
![]()
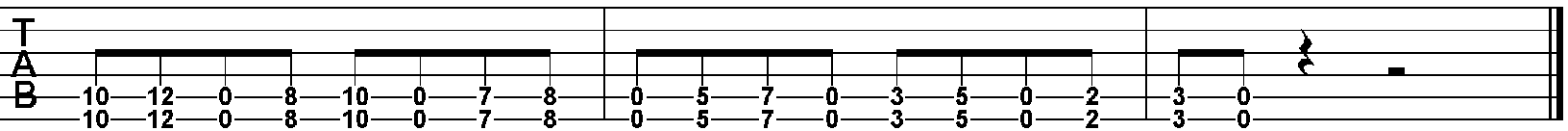
In Example Four I applied the sequence from the prior example to the Blues Scale and ended up with a riff that sounds similar to the riff from a popular Velvet Revolver song.
Example Four:
![]()


Of course, you aren’t locked into playing only chords – you can also play single notes from the scale patterns to create riffs.
Example Five combines single notes and power chords using the notes from both the D Natural minor and Blues Scales.
Example Five:




Free high quality guitar lessons like this one available at: http://paultauterouff.com/freeguitarlesson.php
I hope you enjoyed this lesson. Grab your guitar and try using the patterns and concepts in this lesson to create your own cool-sounding riffs. Mix and match and don’t be afraid to experiment. I am confident you will come up with some great ideas!
Until next time – take care and have fun!
Your Friend,
Paul Tauterouff
©2010 Paul Tauterouff All Rights Reserved.
About The Author: Paul Tauterouff is a professional musician/ guitar teacher in New York. For more information visit Paul’s website at http://paultauterouff.com.
